What is actually a neural network?

The simple idea behind machine learning is to describe given data with a math function. Why? Because math functions allow us to get outputs for unknown inputs (e.g., those, which we’ve never trained on). Let’s recall a linear regression as the basic approach for that:

So we’re trying to draw a line (in other words - find a function) that has the shortest distance between itself and all data points. Now when we have a continuous line, not just a set of points. And now we can find Y (predict an output) for any X (given input), even for new points (which were absent in the initial dataset).

In ML such a line is called a model, but let’s remember that it’s still just a math function.

Complexity growth

Let’s imagine a more complex situation. Suppose we have the following set of points to build a model (a math function) for:

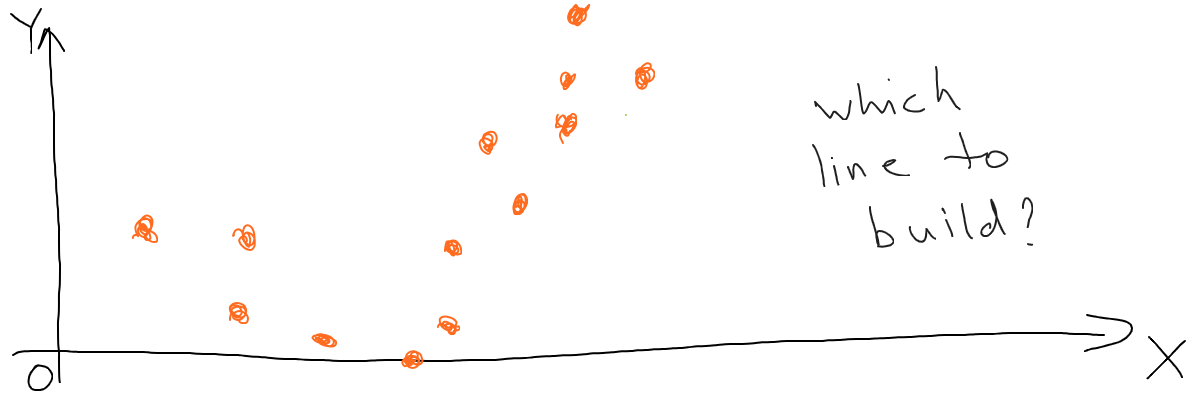
Now if we try to fit a line into this dataset, we end up building a very poor model no matter how hard we try.

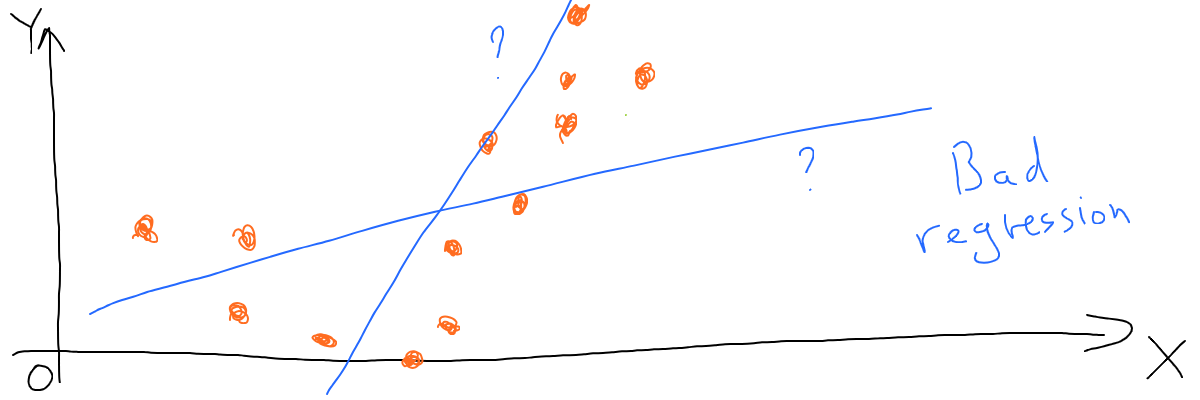
Why? Because our model lacks some features - the line is straight, while what we need is something like this:

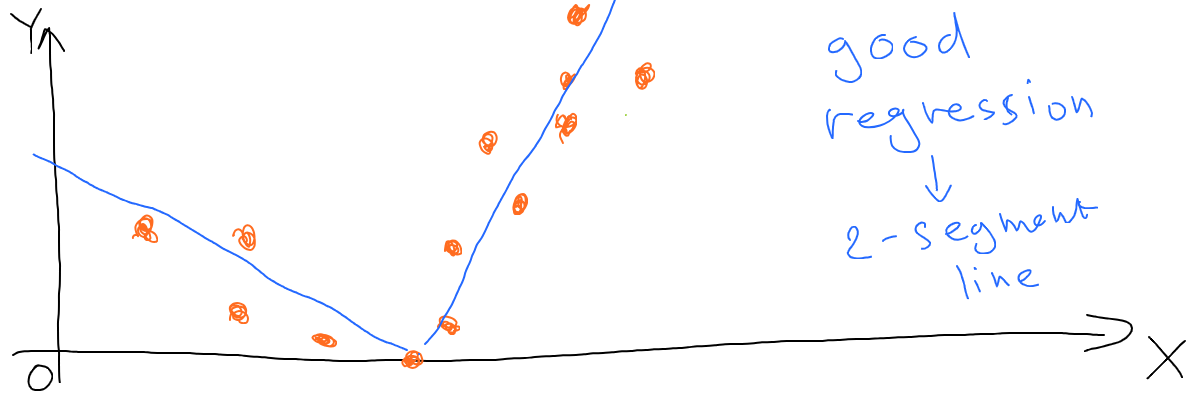
And math can help us build this kind of line by using multiple straight lines and one more function.

ReLU and multiple segment lines

It’s easy to see that our desired lines consist of 2 segments, each is basically a part of a straight line. And each of those straight lines can be described by a separate math function:

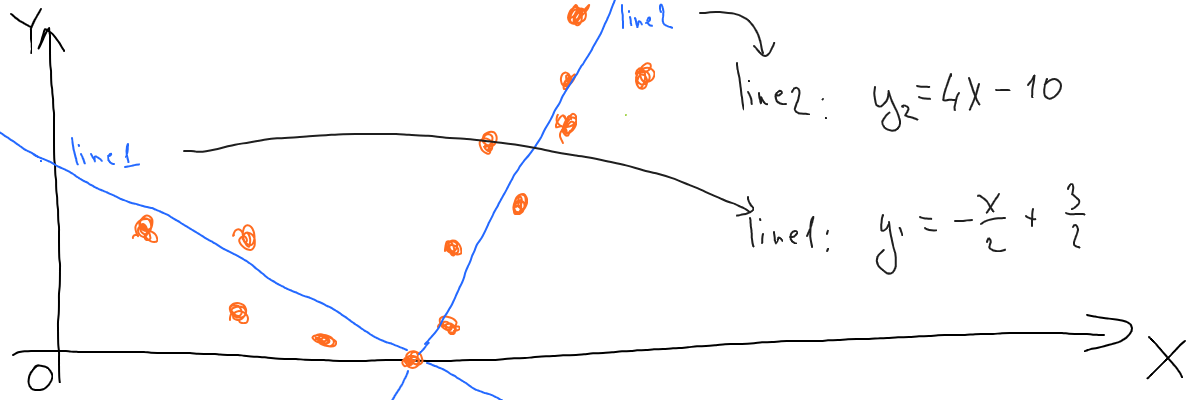
Where did those y1 and y2 functions come from? Well, any function could be used here, I’ve just tried something that looks like those blue lines.

Now we can use a special function to combine those 2 straight lines and get a single line of 2 segments. And that function is called ReLU. This is a super simple function that returns all positive values and zero for all negative values of input:

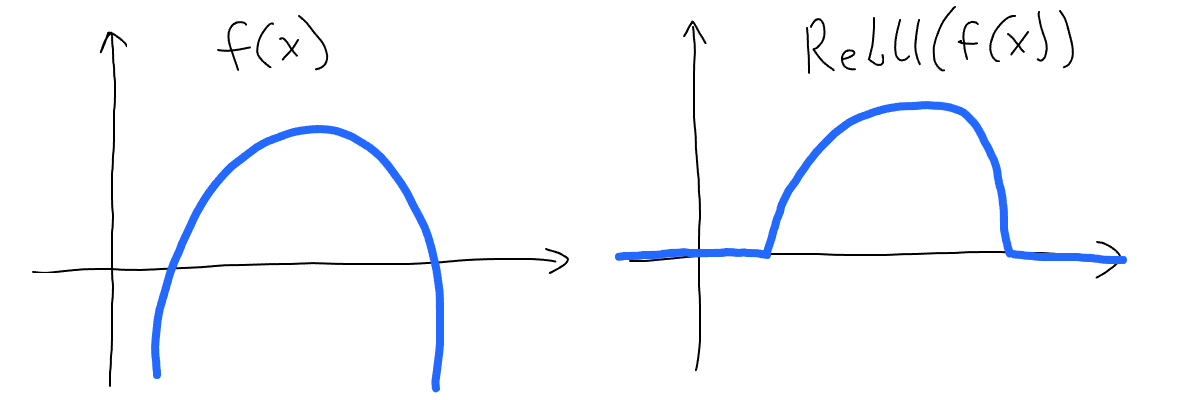
Let’s build a ReLU function for both of our straight lines and see how that looks:

Now if we simply add those two ReLU functions and chart them, we get the following:

This is exactly what we wanted to get - a multiple-segment line that is described by a math function. It fits our data just fine, so this is actually our ML model:

We can, of course, combine more than 2 functions using ReLU to achieve even more complex forms of lines. So what has a neural network to do with that?

Neural network

It’s a very common approach to visualize neural networks using neurons and connections between them:

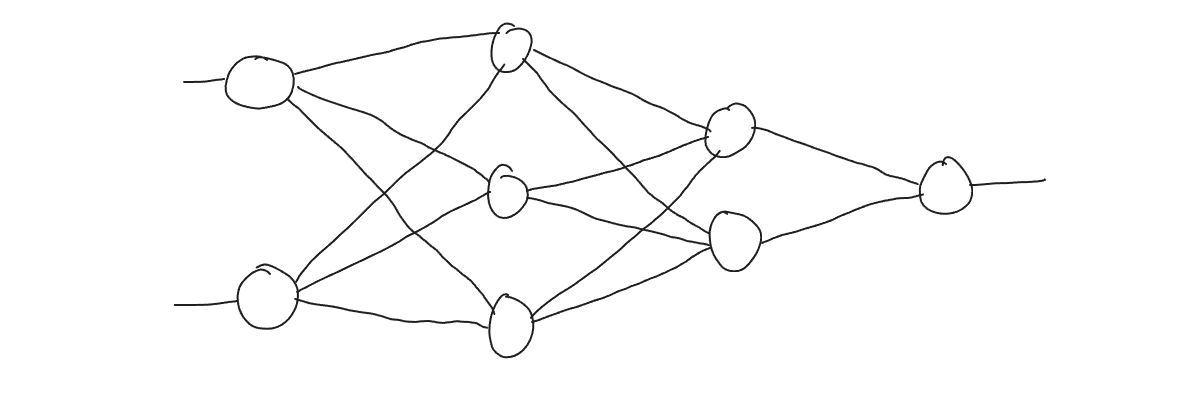
But this is not a neural network, this is a neural network structure (or architecture). A neural network is exactly the line we got in the previous example:

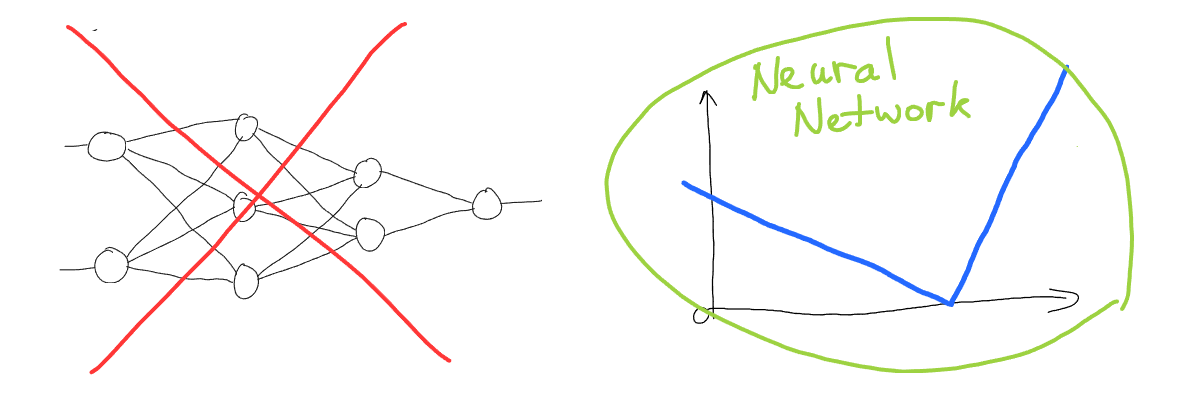
Now let’s visualize our line schematically:

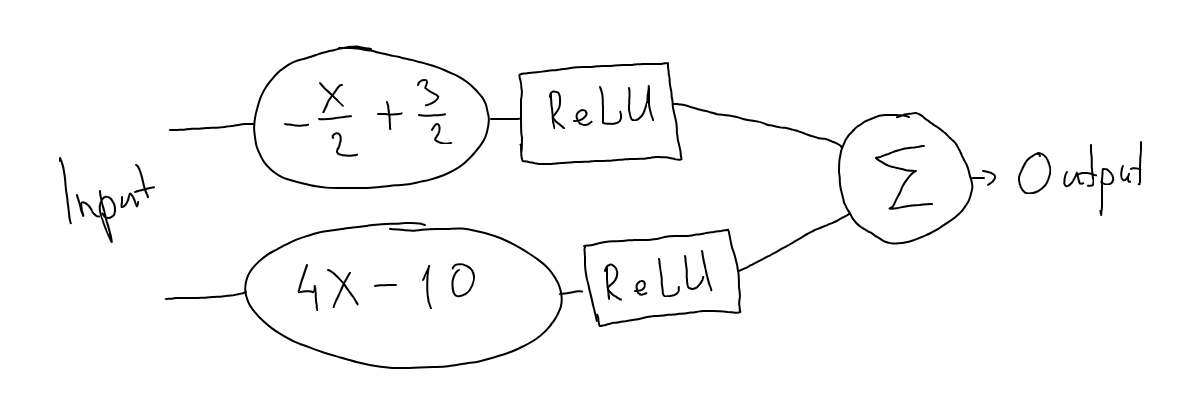
And this is what’s called a structure (or an architecture) of a neural network. So each separate line function represents a neuron, and a ReLU function represents the connection between neurons. But at the very core - a neural network is still just a complex multi-segment line (or high-dimensional surface in a high-dimensional space).

Neural network layers

A powerful feature in neural networks is the ability to add layers:

Let’s see what it means in terms of math, let’s add an additional layer to our initial multi-segment line (with random line functions from the top of my head):

Note how we used z in the new layer function so as not to confuse it with input x because the second layer receives into input what comes from the first layer as output.

Now let’s write it down in a math form:

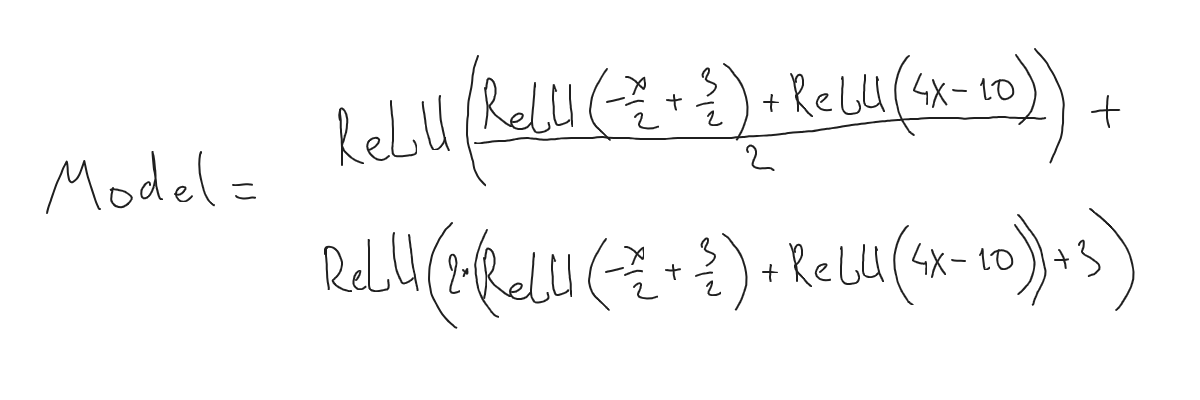
Looks not too good, that’s why people mostly prefer a schematic way. Let’s also chart our new neural network:

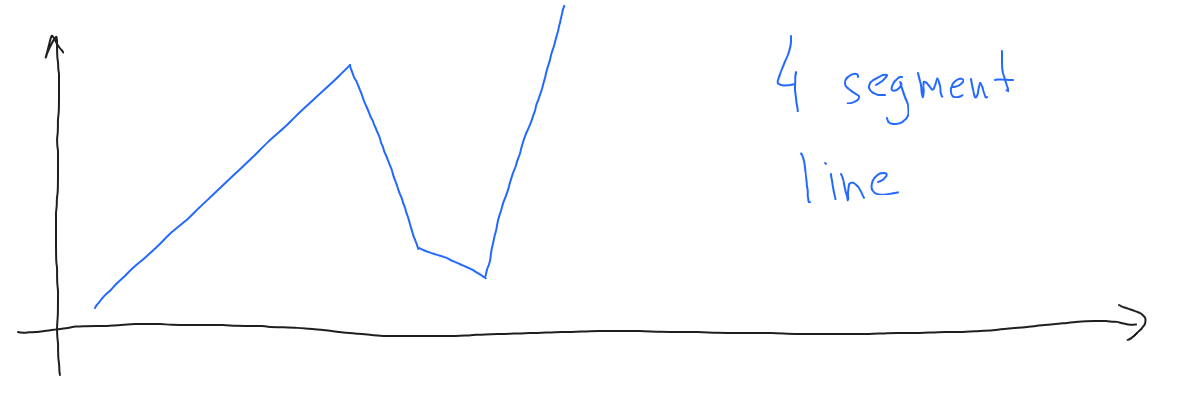
In other words, the new layer increased the number of line segments. This enables our model to work with more complicated data.

Long story short

Neural Network - is a multi-segment line (hyper-surface), not some connected circles. ReLU (but not only this function) is a way to build a multi-segment line. This is important to better fit to data. Neural network layers increase levels of line (hyper-surface) complexity to further fit to more and more complicated data.