Matrices and vectors math for AI with Python examples

Vectors and Matrices math is one of the basic tools used for AI. There’s a lot you can do with vectors (and matrices, tensors, and so on). Linear algebra is a good place to master vectors, but let’s take a look at popular basic stuff that can help in a lot of cases.

What are vectors and why do we use them

Vector is a point in (some) space, which we are “looking at” from (some) point (usually zero point). In simple 2-dimensional space, vectors look like this:

We have 2 vectors here. Each is described by 2 coordinates — x and y. Vectors are usually written down as:

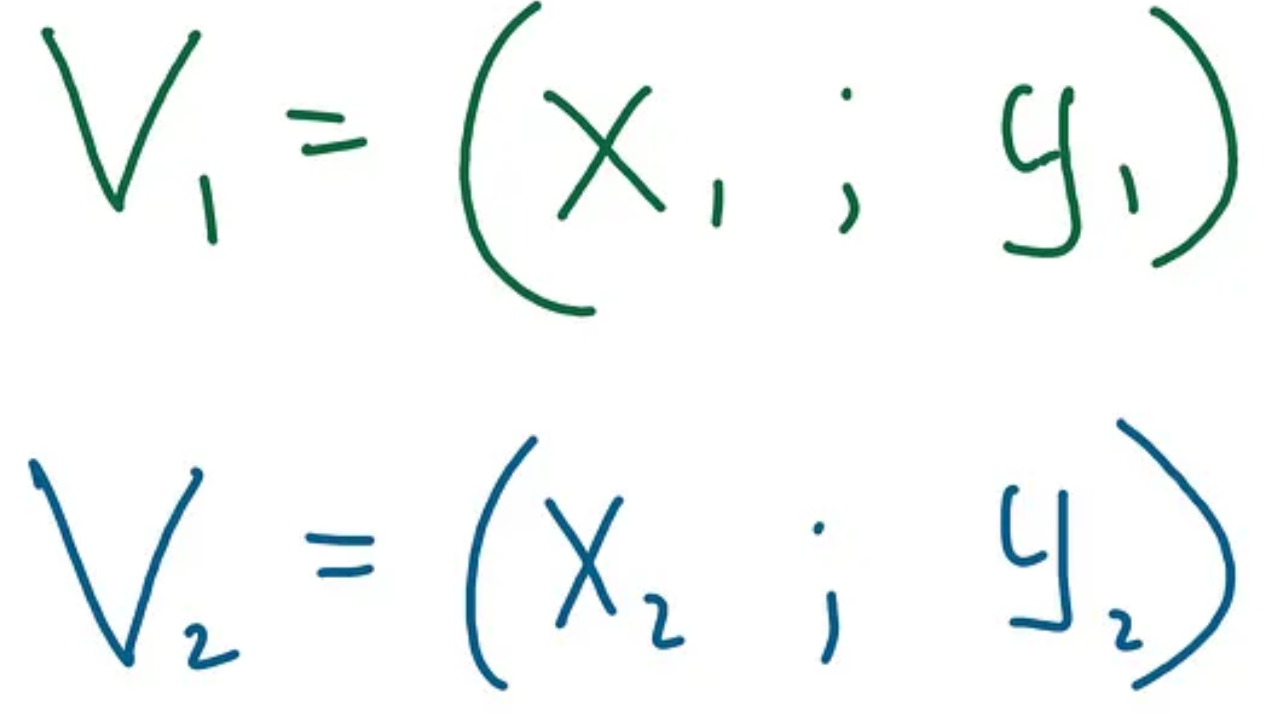
Vectors can have more than 2 dimensions. For example, 3-dimensional vector will look like this:

More dimensions will be harder to draw, but we basically can have any number of coordinates for vector:

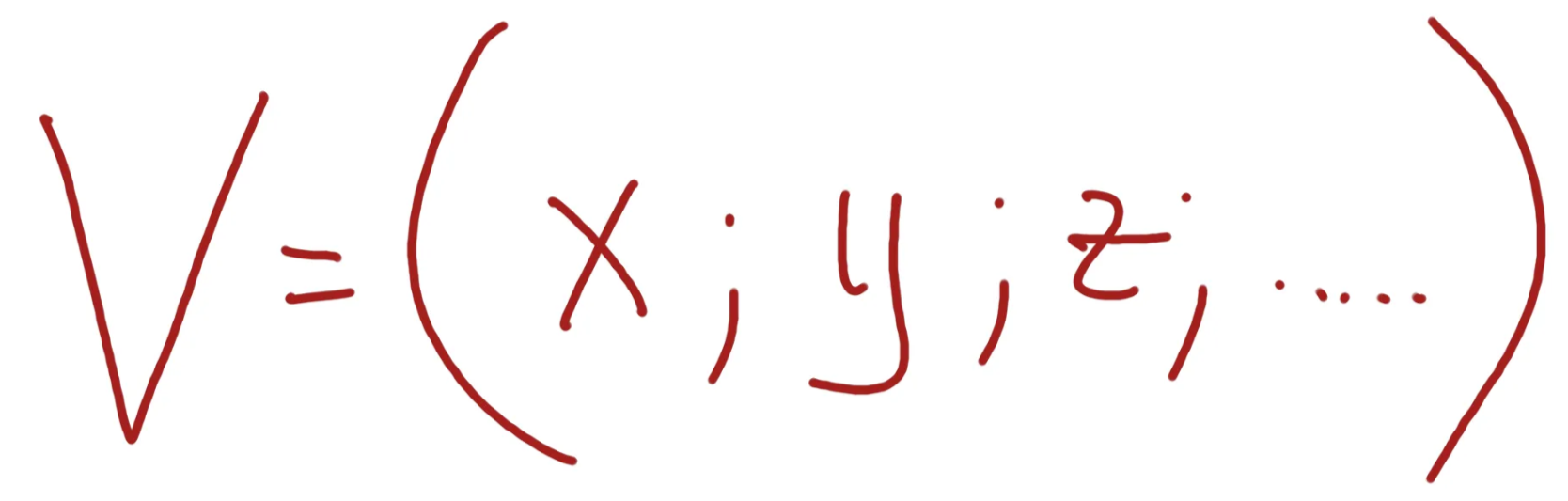
Now let’s imagine, that we have a set of people that we want to analyze. Each person is described by several features - age, weight, and height. We can, in the language of math, say that we have a set of vectors in 3-dimensional space:

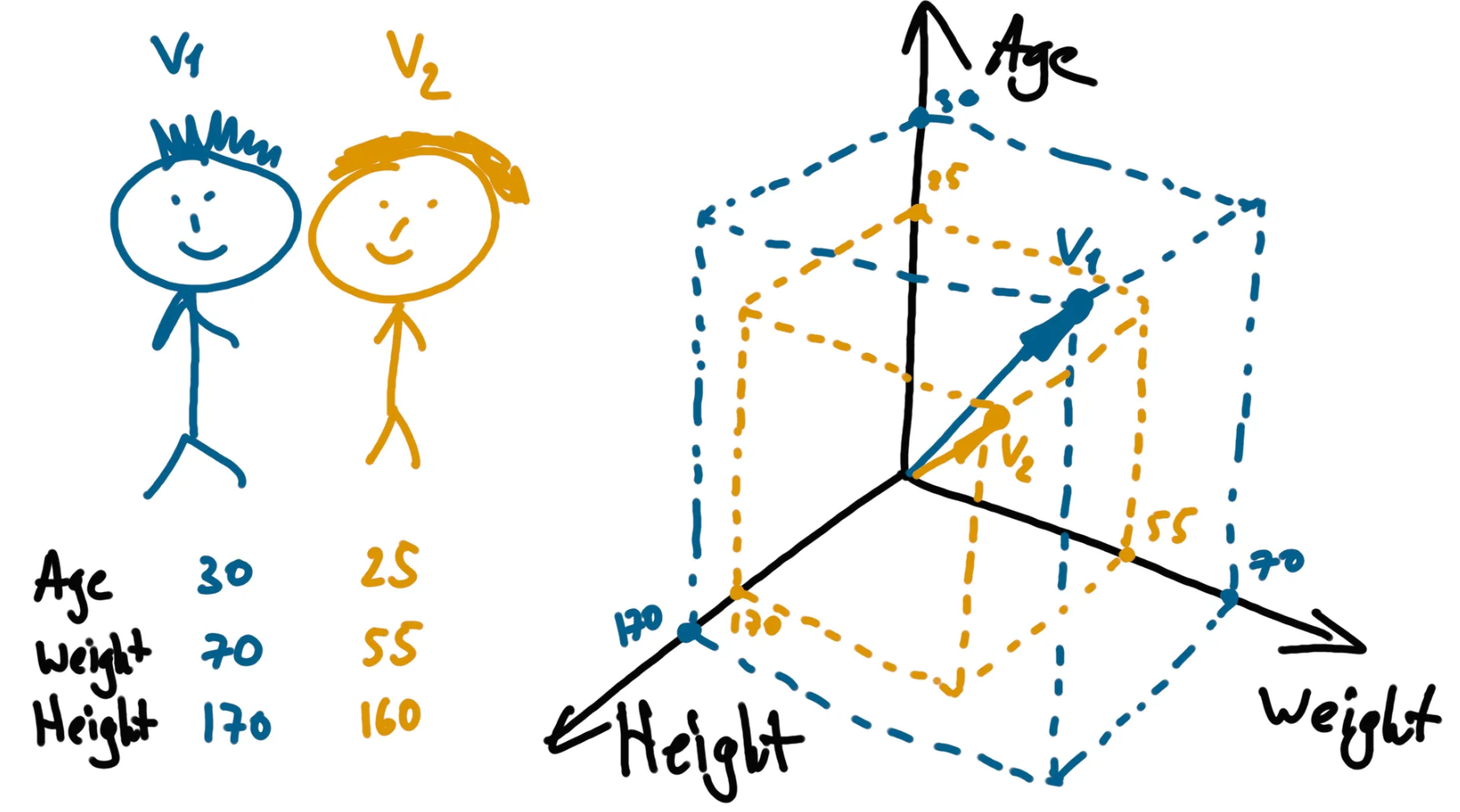
So it’s easy to write down a list of observations (people in our case) with features (age, width, height in our case) as vectors:

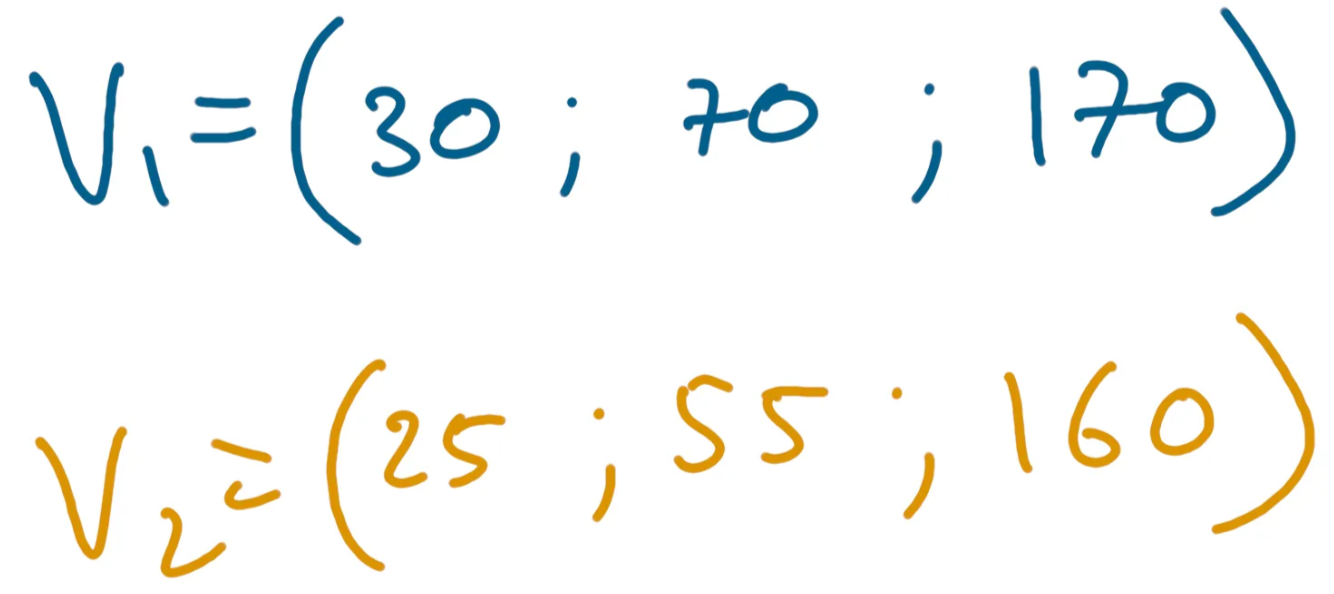
And this means we can apply vector math to analyze our data. And vector math has a lot of powerful tools. But before looking at math operations, let’s discuss another structure, called a matrix.

Matrices are also vectors

Matrix — is a set of vectors. Easy. Let’s imagine a vector, called M, which has V1 and V2 (two vectors from the previous example) as coordinates:

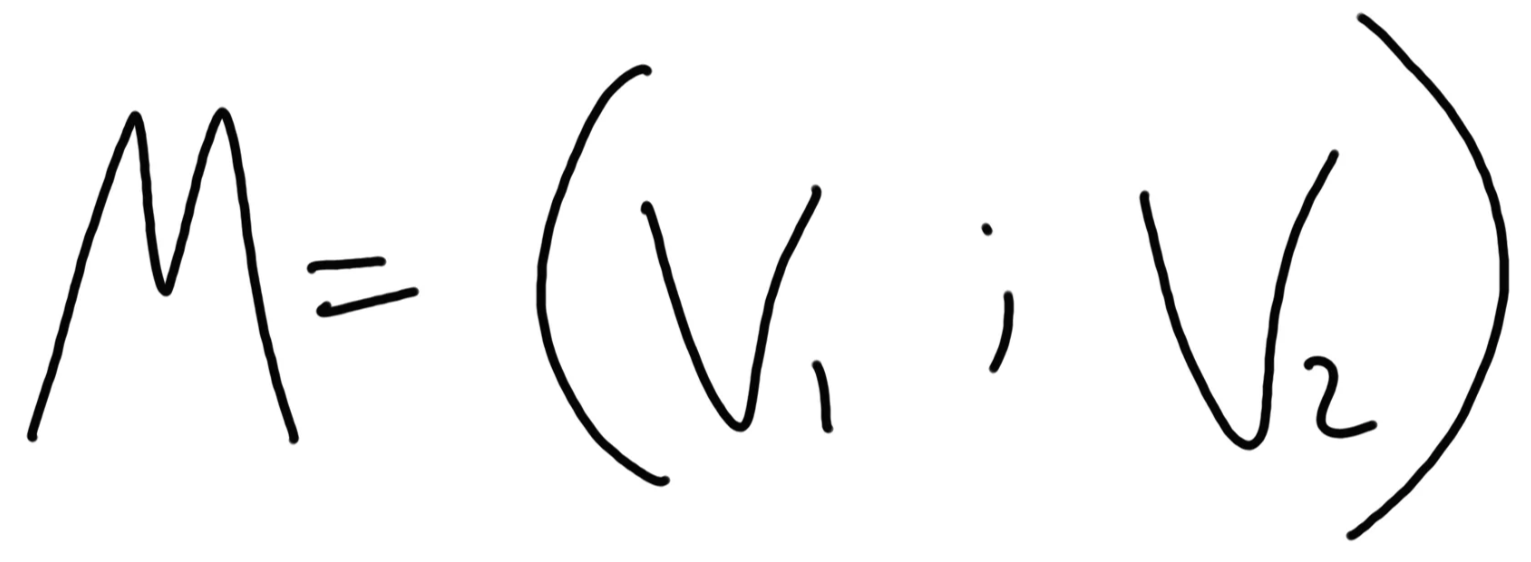
This is called matrix. We can use another, more popular, form to write the matrix down:

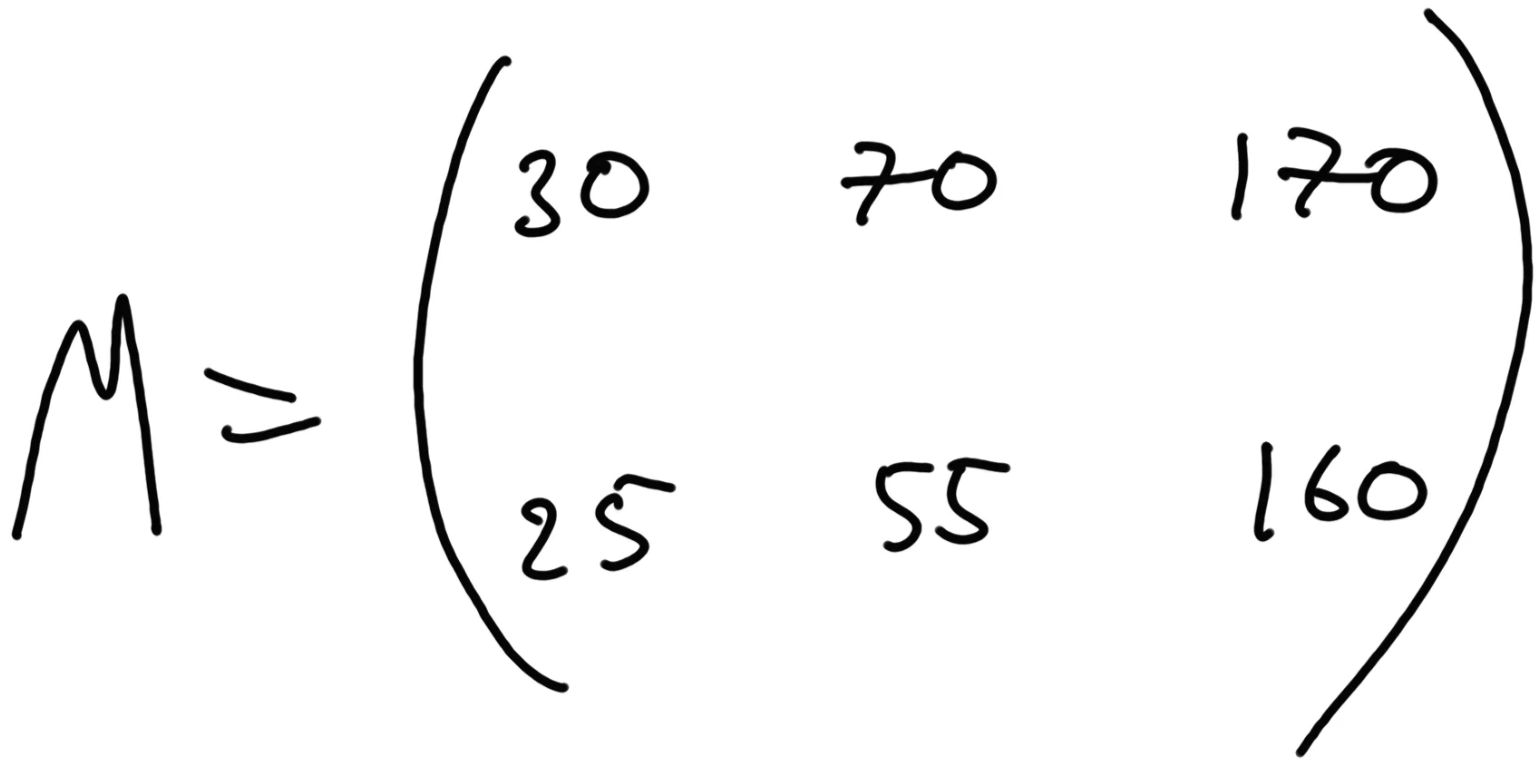
We say that this matrix has 2 dimensions — 3 columns and 2 rows, so the form of the matrix is 3x2. Matrices can have any number of dimensions and be of any form. Example of 3-dimensional matrix 2x2x3:

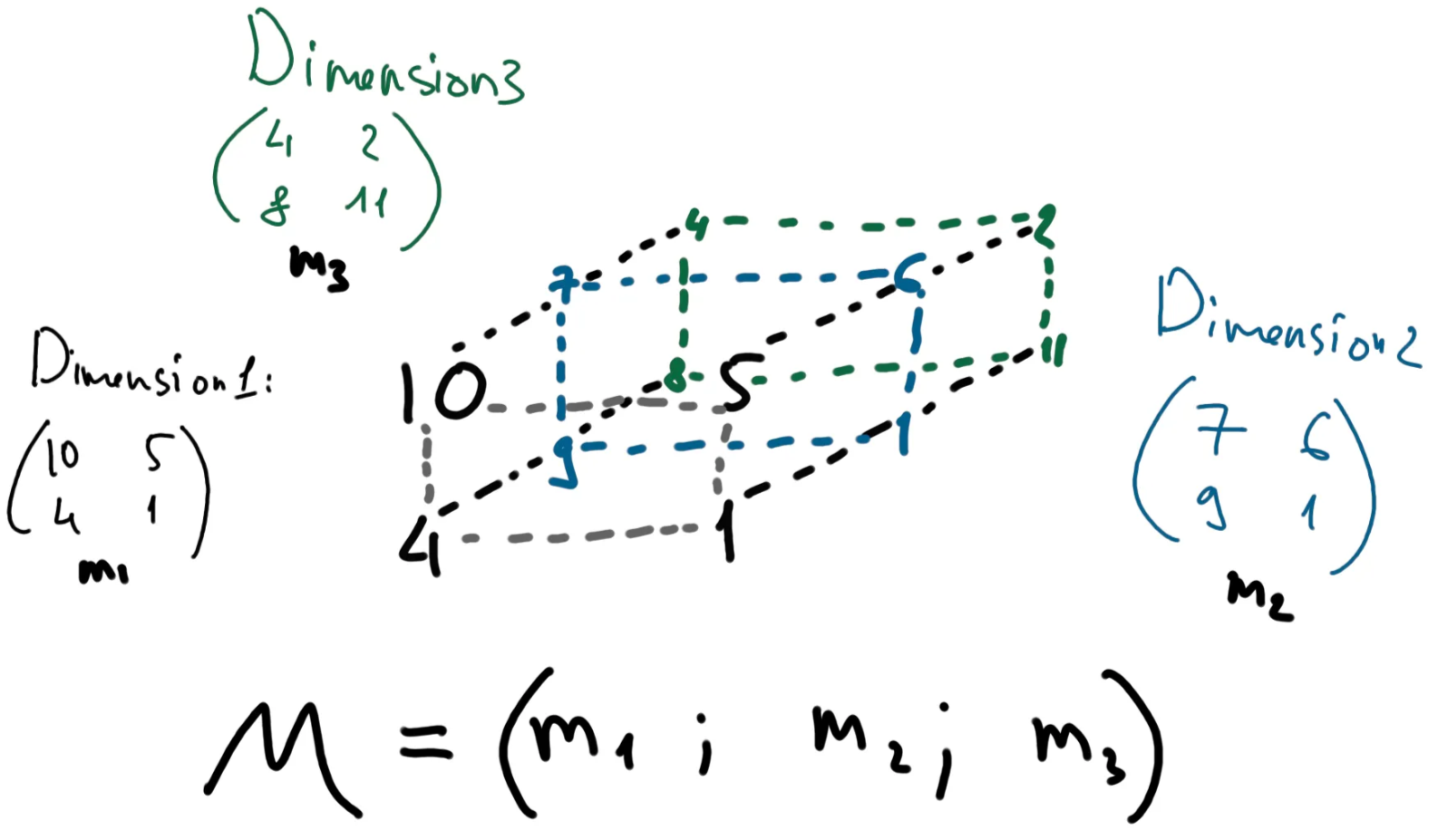
So, a 3-dimensional matrix is a vector of 2-dimensional matrices. And, as we remember 2-dimensional matrix — is a vector of vectors. So 3-dimensional matrix is a vector of vectors of vectors. And this means, everything comes down to vector math.

Let’s look at some basic vector/matrices operations.

Euclidean norm (distance)

Euclidean norm (or distance) is a way to calculate the mathematical “length” of a vector. It is calculated as:

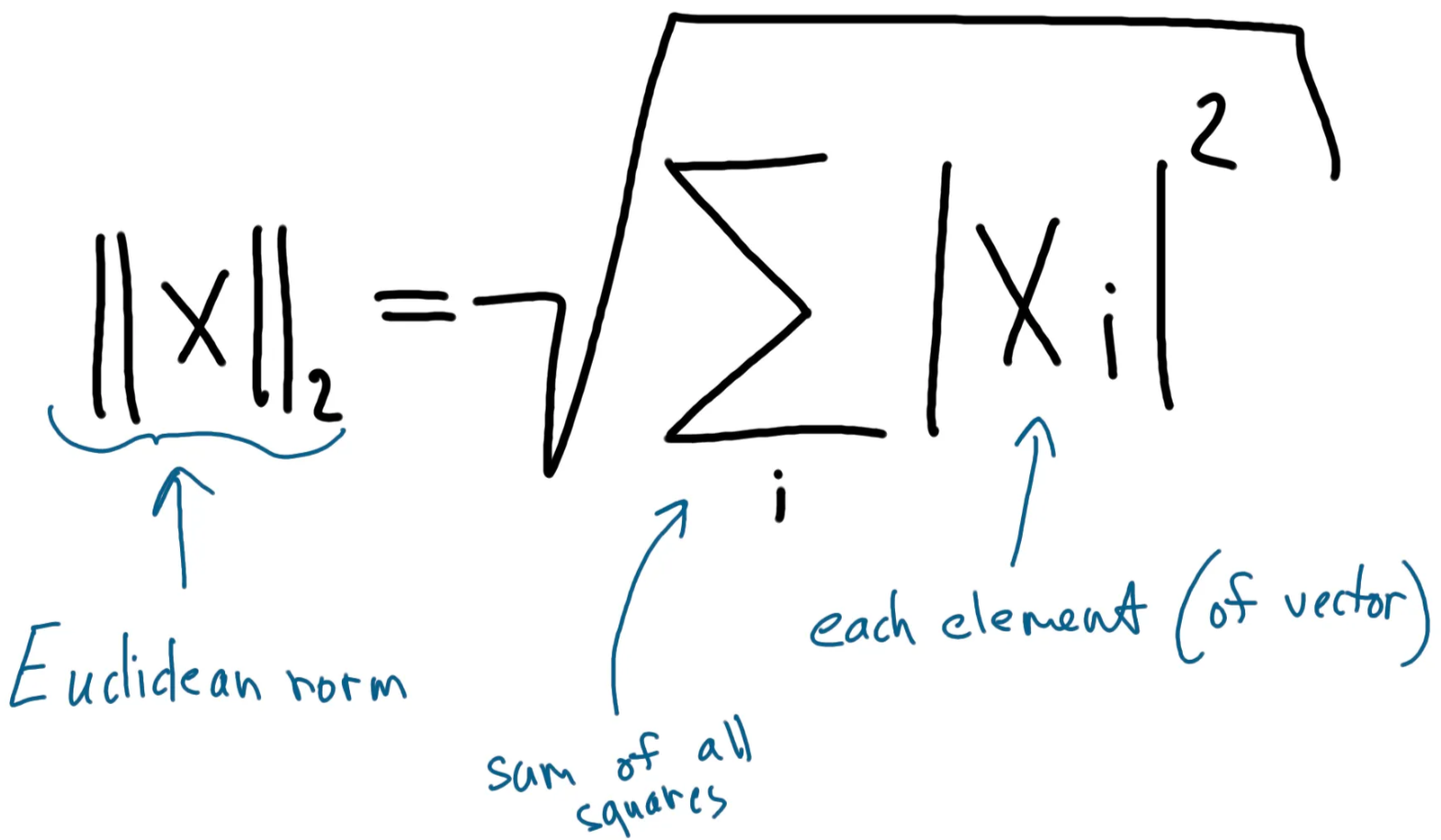
In Python, this can be calculated using the Numpy package. Let’s find euclidean distance for a sample vector (1, 2, 3):

import numpy as np

a = np.array([1,2,3])
dist = np.linalg.norm(a)

print(dist)

3.7416573867739413

• import numpy as np — import Numpy module
• np.array([1,2,3]) — define Numpy array
• np.linalg.norm — return Euclidean norm for a given array

Adding vectors or matrices

To add 2 vectors, we have to add all corresponding elements of our vectors:

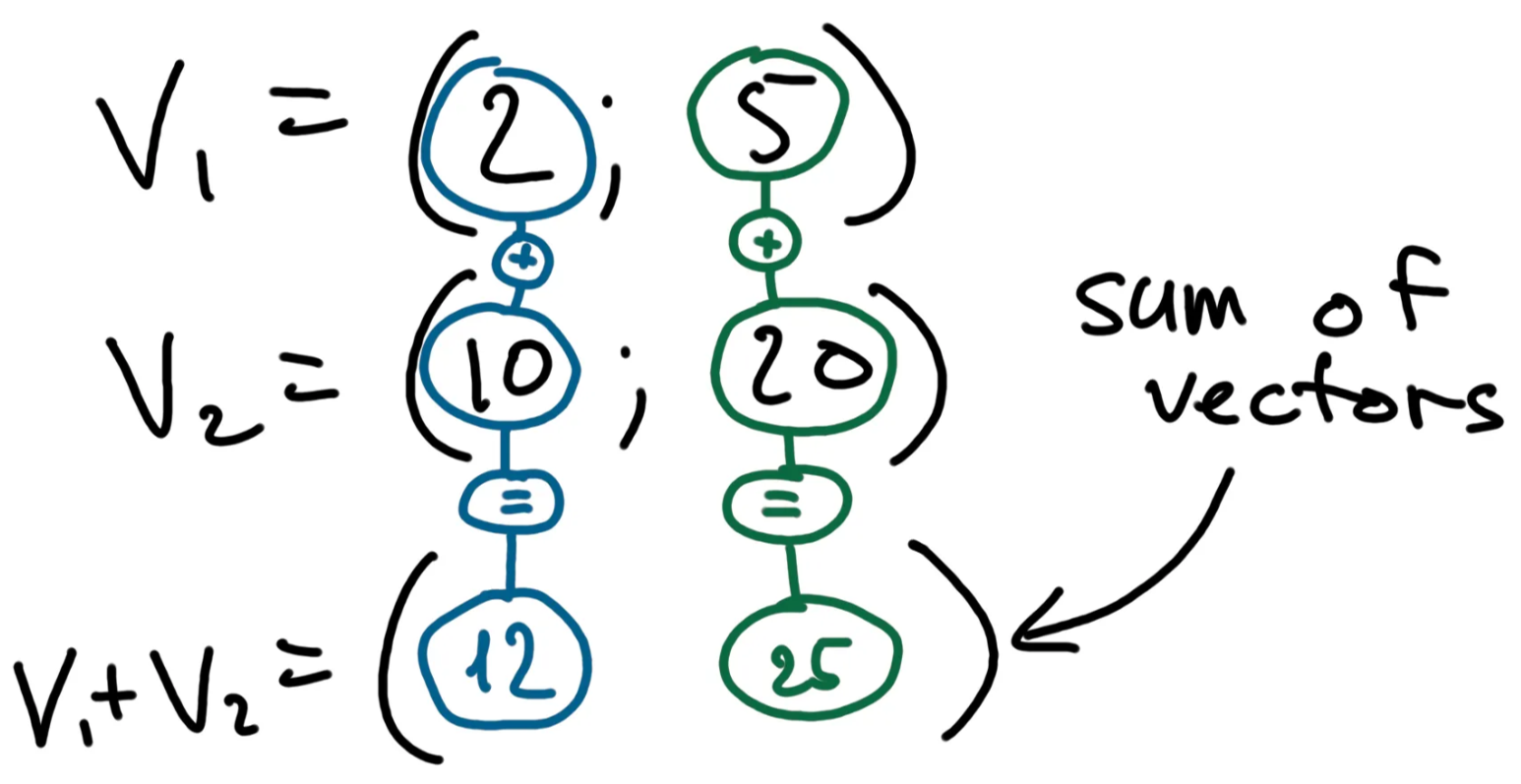
In Python, you can just use the standard + operator to add Numpy-defined vectors:

import numpy as np

a = np.array([1,2,3])
b = np.array([10,20,30])
sum = a + b

print(sum)

[11 22 33]

• a + b — we can use + with Numpy arrays to add them
• sum — will also be a Numpy array

Because, as we know, matrices are also vectors, to add 2 matrices we have to add each element of our matrices:

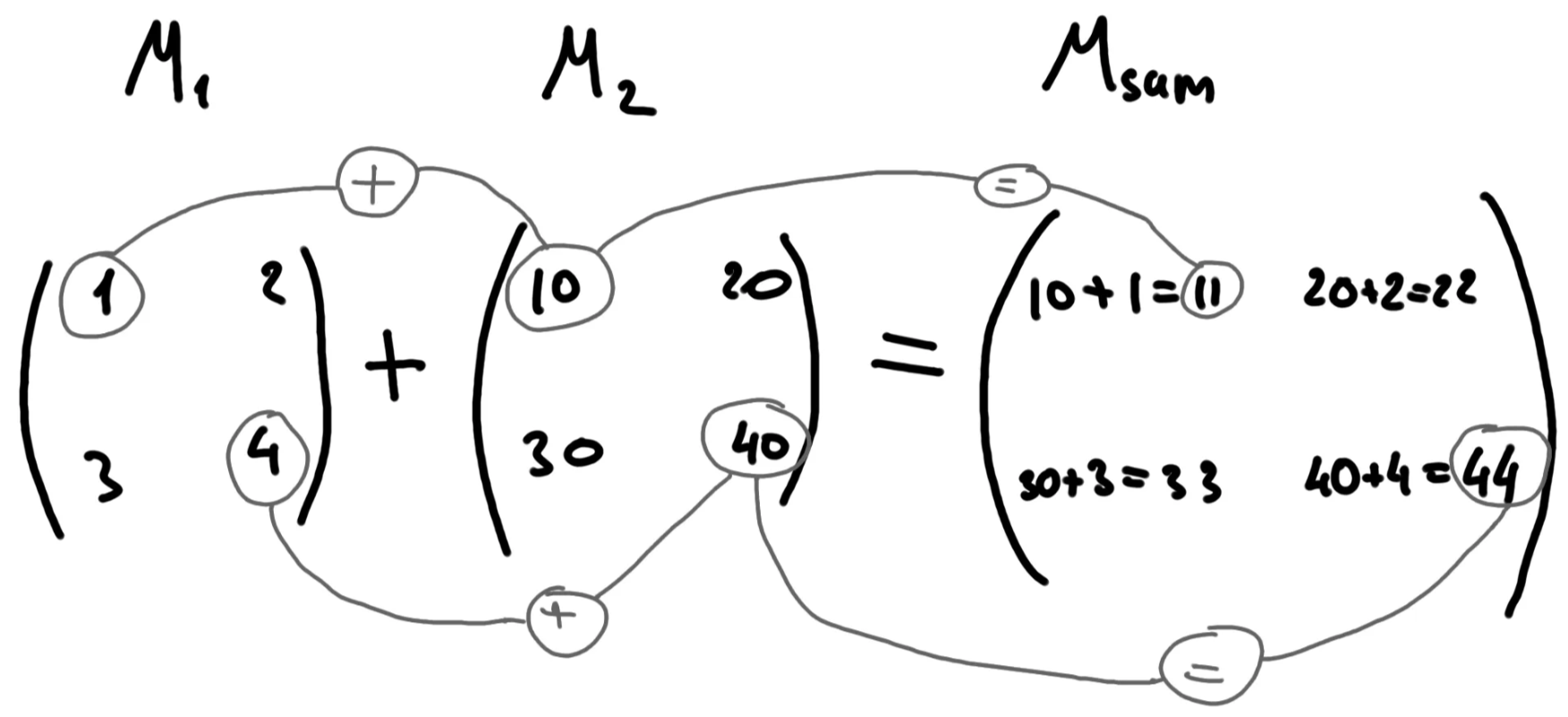
The same approach to add matrices in Python — just use the + operator:

import numpy as np

a = np.array([[1, 2 ], [3, 4 ]])
b = np.array([[10,20], [30,40]])
sum = a + b

print(sum)

[[11 22]
 [33 44]]

• sum = a + b — if a and b are matrices, sum is also a matrix

Matrices multiplication

This is somewhat tricky. To multiply 2 matrices we have to calculate the sum of row/column value products for each element of the resulting matrix:

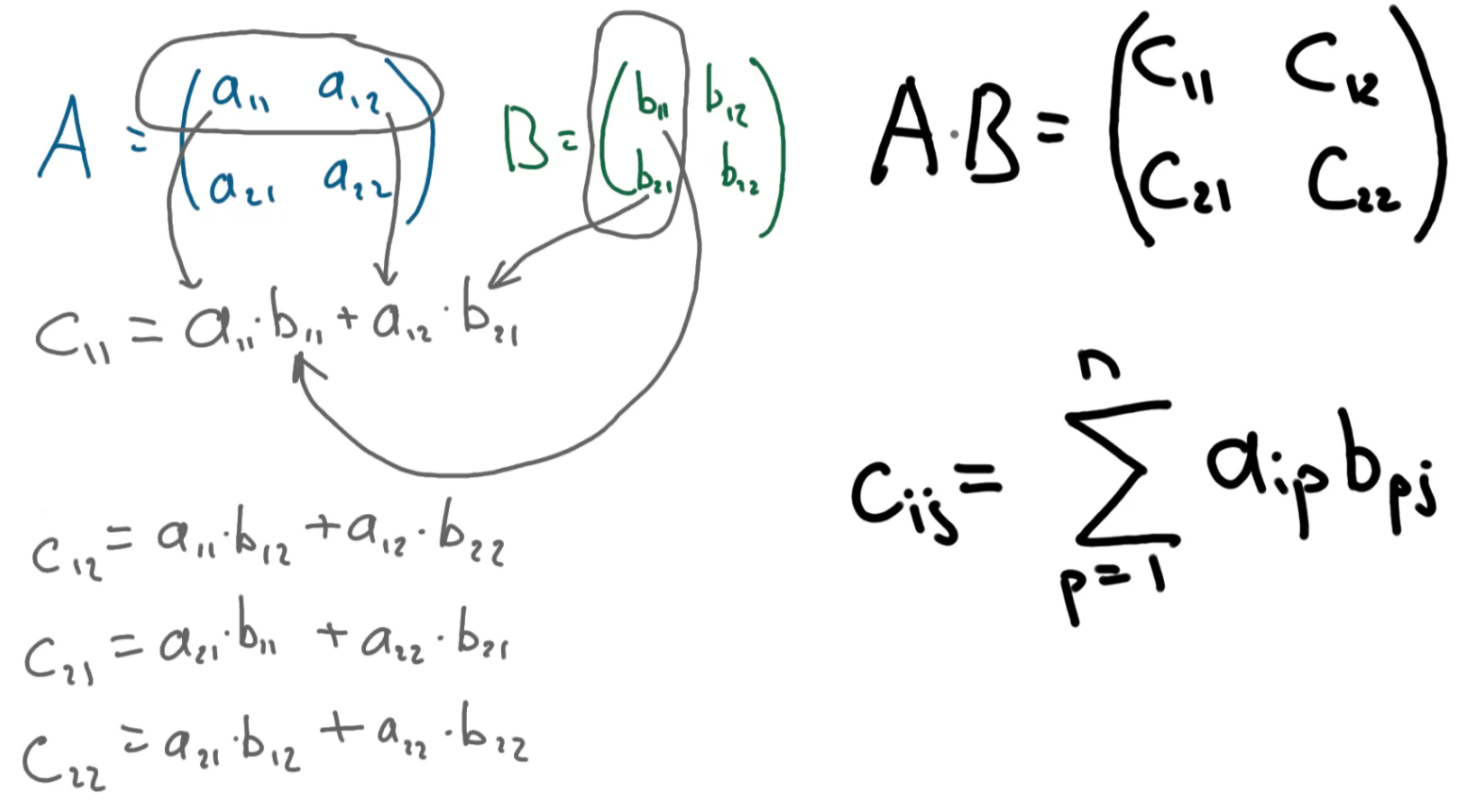
So each element of the new matrix is a sum of the products of corresponding elements of rows from the left matrix and columns from the right matrix. Note, that:

1. You can only multiply matrices where the number of left matrix columns is the same as the number of right matrix rows.
2. Resulting matrices can be of a different form than source matrices (if they have a different number of rows and columns).

There’s a special @ operator in Python to multiply matrices:

import numpy as np

a = np.array([[1, 2 ], [3, 4 ]])
b = np.array([[10,20], [30,40]])
ab = a @ b

print(ab)

[[ 70 100]
 [150 220]]

• a @ b — multiply a and b Numpy matrices

Transpose matrix

Transposing matrix is a popular operation as well. To transpose a matrix we just have to change its columns to rows (and rows to columns). In other words — “mirror” it:

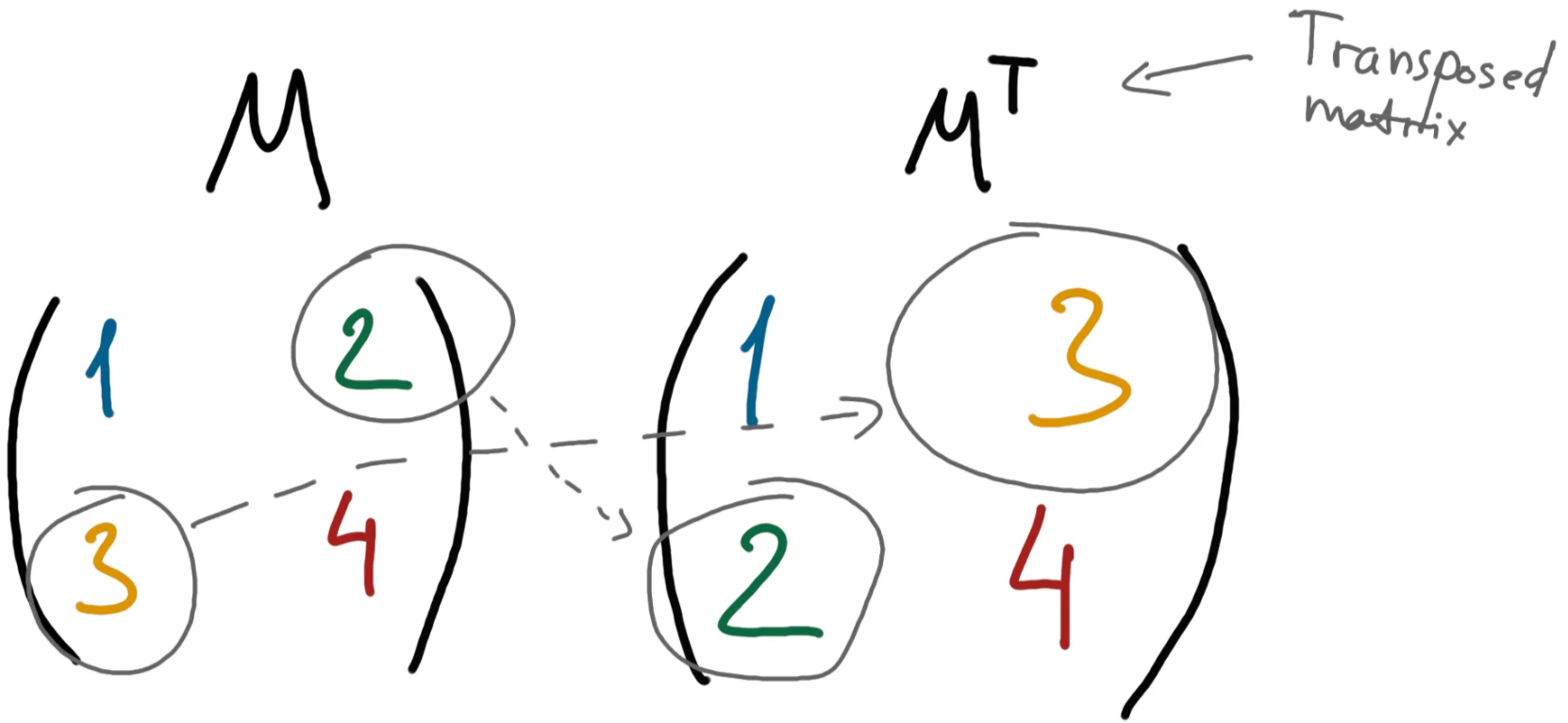
Each Numpy matrix in Python has .T property which returns transposed matrix:

import numpy as np

a = np.array([[1, 2 ], [3, 4 ]])

print(a.T)

[[1 3]
 [2 4]]

Matrix determinant

A matrix determinant is a tool to research a system of equations based on our matrix. It’s calculated in multiple iterations:

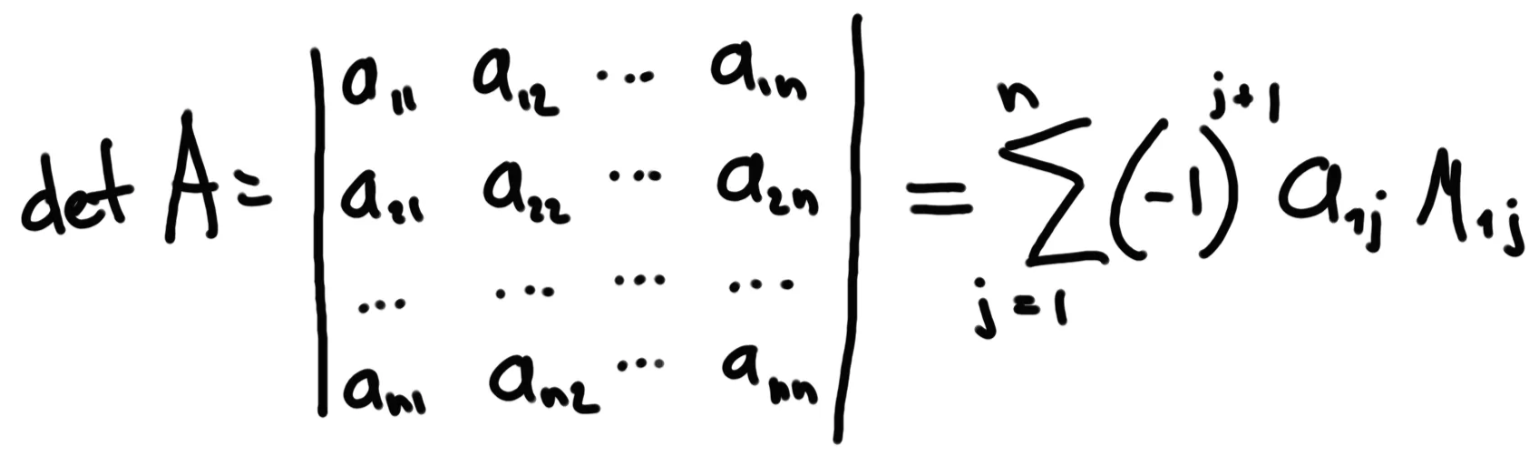
So we have to iterate down to 2x2 matrices from our bigger matrix. For 2x2 matrix determinant is simply calculated as:

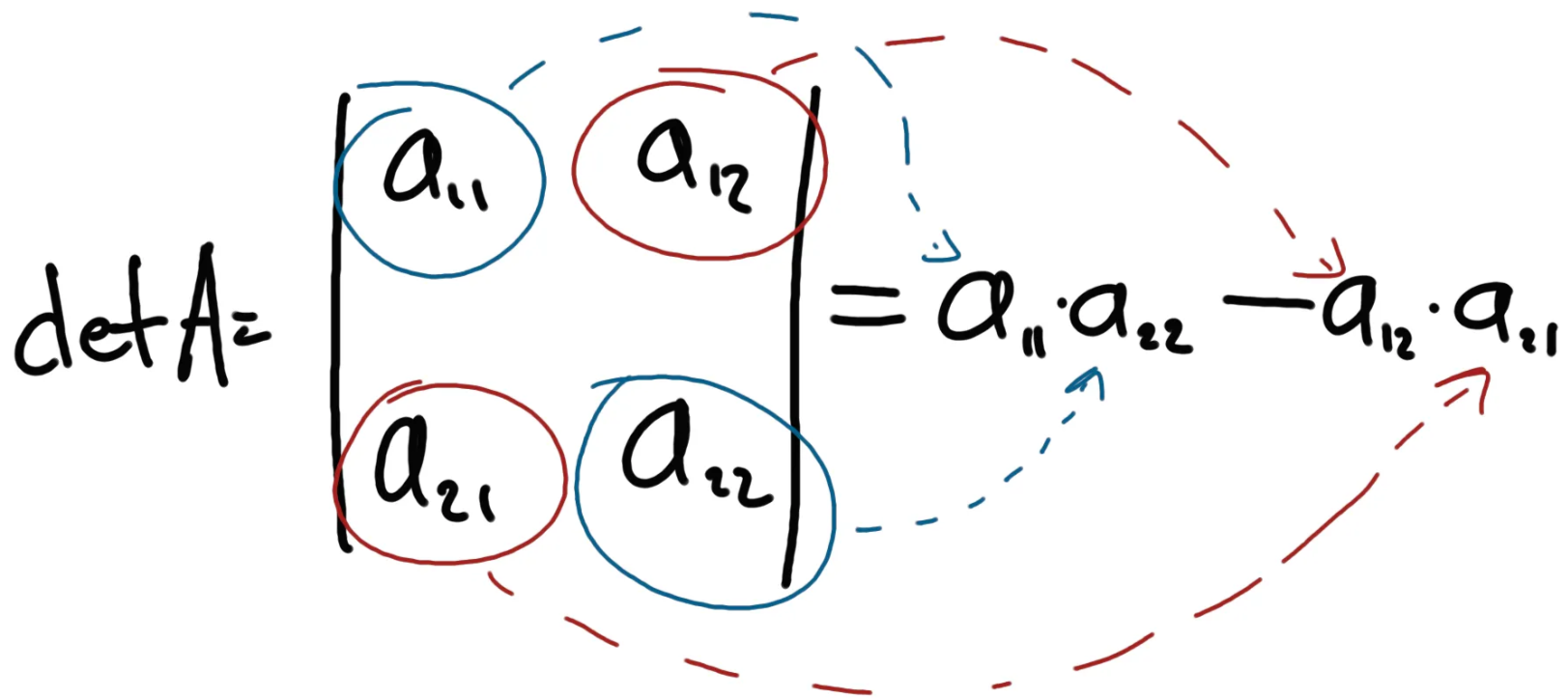
In Python, we can use lingalg.det() method to calculate matrix determinant:

import numpy as np

a = np.array([[1, 2 ], [3, 4 ]])
det = np.linalg.det(a)

print(round(det))

-2

Matrix rank

Matrix rank is the maximum number of linearly independent columns (or rows) of a matrix and can be calculated in Python:

import numpy as np

a = np.array([[1, 2 ], [3, 4 ]])
rank = np.linalg.matrix_rank(a)

print(rank)

2