Creating a bigram language model for text generation with Python

A bigram language statistical model is a language model that predicts the likelihood of a word given its preceding word. In other words, it models the probability of a word occurring based on the word that precedes it.

The idea behind the model is that when we have a lot of text to train on, the likelihood of generating appropriate words is quite high and we can achieve relatively good results for text-generation-related tasks.

Let’s take a closer look at the ideas and go through the implementation example using Python.

What is a bigram

Let’s take a look at this text:

Bigrams are just every two words in these sentences coming one after another:

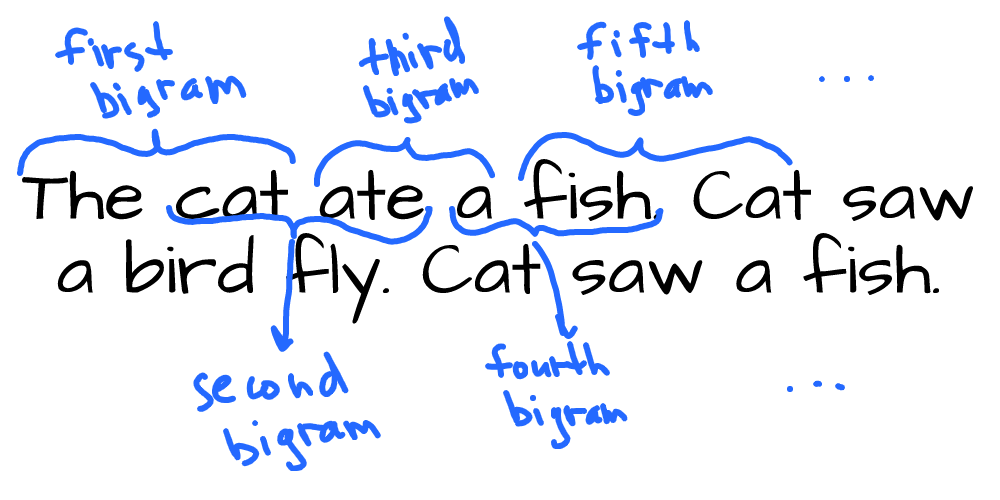
So all bigrams from the given text would be a list of the following word pairs:

We can see 13 bigrams we could generate from our text. At this point, this doesn’t give us anything, but we need to understand the definition of bigrams to move along. So, bigrams are just all pairs of consecutive words from the given text.

Bigram is a subset of a more general Ngram concept. Where N stands for the number of words we deal with.

For example, if N is 1, we deal with unigram, which is just a single word. Unigrams for our text will include “The”, “cat”, “ate” and so on.

If N is 3, we deal with trigram, which is, as you might guess, 3 words in length. Trigrams for our text will include: “The cat ate”, “cat ate a”, “ate a fish” and so on.

Ngrams are not limited to words, we can actually use any object here. For example, we could choose to work with chars instead of words. In this case, our char-based bigrams for our text would include individual letters instead of words: “Th”, “he”, “e_”, “_c”, “ca”, “at” and so on (“_” symbol stands for space).

But let’s return to word-based bigrams and see what we can engineer here.

The idea behind the statistical language model

Let’s consider the following question: if we take the word “cat”, then based on the given bigrams, what words might come after this word? We can see multiple bigrams starts from the word “cat”:

We can see that our text has 3 relevant bigrams. Two of them give us the word “saw”, and one gives us “ate”. Now, we can say that the cat either saw or ate something, and it’s 2 times more likely that the cat saw something that ate something:

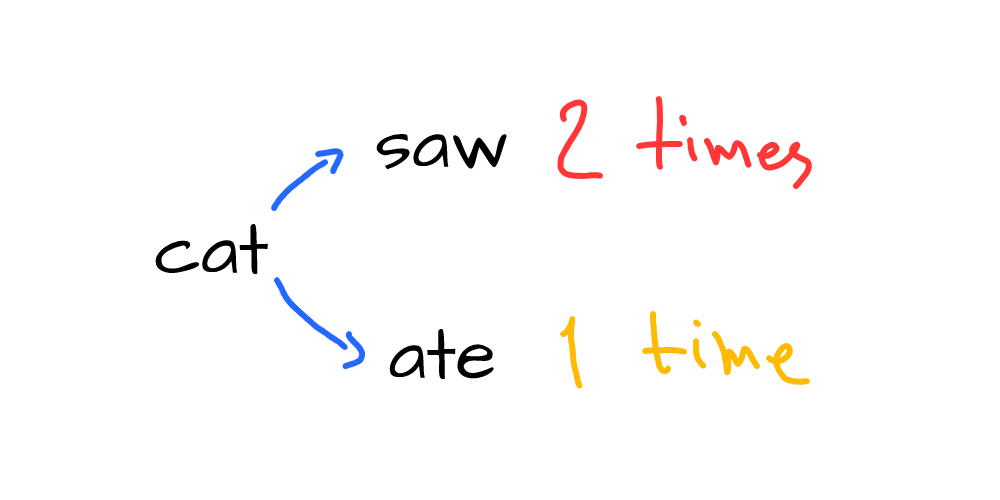
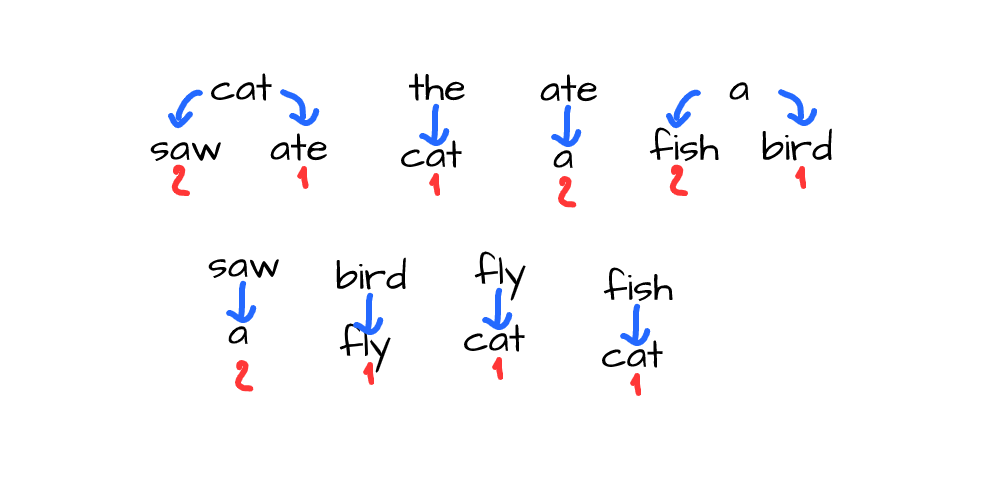
Now let’s collect the same stats from all bigrams in our text. So we will have a table with the all unique words that go first in all bigrams, and the count of all possible second words:

Now let’s do the following - take a random starting word from this set and pick one of the possible second (following) words. Then repeat, by taking that picked word and finding bigrams where it’s the first word. Then take one of the second words from found bigrams:

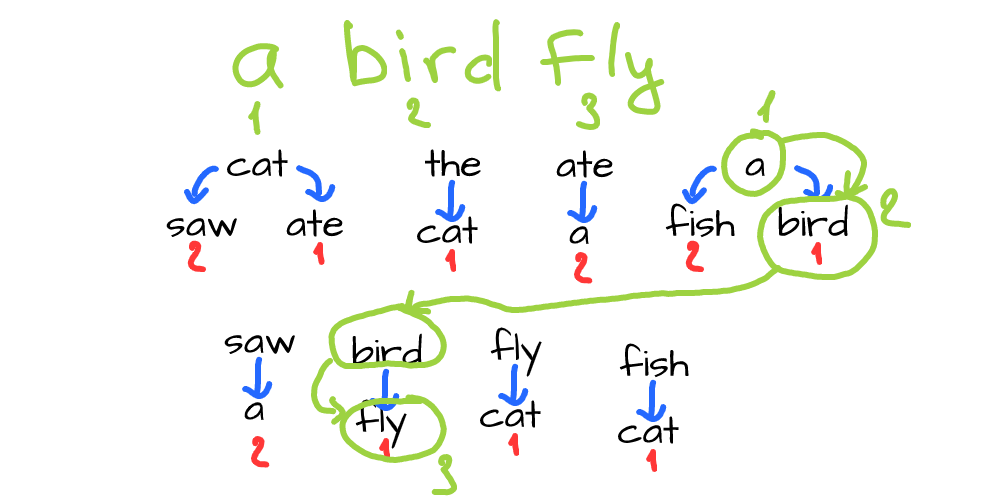
Here we have chosen “a” as a starting word. Then we have chosen “bird” from two available options (“bird” or “fish”). Then we located “bird” as a starting word in one bigram and chose “fly” since this is the only word available. And we have actually generated a sentence that makes some sense.

This is exactly the idea behind the bigram statistical model - we collect bigram statistics from a text and then randomly generate sentences by predicting the next word based on the previous one:

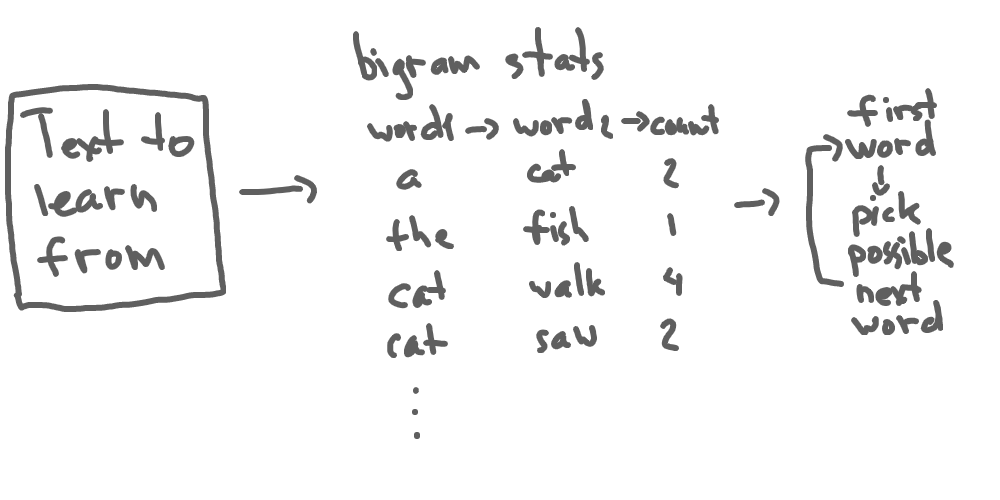
Creating a bigram model in Python

Let’s program a simple model in Python. We will use the text.txt file to learn from, which is some old book about space.

1. Loading and preparing text data

We start by loading text and doing some preprocessing to filter out all the trash:

text = open('text.txt').read()
text = text.lower().replace("\n", ' ')

import re
text = re.sub('[^a-z0-9\.\-]', ' ', text)
text = re.sub('\s{2,}', ' ', text)
text = '. ' + text.replace('.', ' .')
text = re.sub(' [a-z0-9] ', '', text)

• open('text.txt').read() — read the entire text.txt file (we’re going to learn based on this file)
• text.lower().replace("\n", ' ') — lowercase everything and remove line breaks
• re.sub('[^a-z0-9\.\-]', ' ', text) — remove all non-alpha-numeric symbols to leave only words, numbers, and dots
• re.sub('\s{2,}', ' ', text) — collapse multiple spaces into a single space
• '. ' + text.replace('.', ' .') — add a space to do and add a dot to the beginning of our text (we’ll see later why we need that)
• re.sub(' [a-z0-9] ', '', text) — remove all single characters words from the text, as they might create a lot of noise

At this point we have the text variable with an entire text from our book.txt file, let’s print the first 100 characters of this variable:

print(text[0:100])

. this book isthreefold invitation to the philosophy of space and time . it introduces gently and si

2. Creating bigrams and calculating stats

Now we split our entire text into words and calculate first/second word pairs:

words = text.split()
bgrams = {}
for i in range(len(words)-2):
  w1 = words[i]
  w2 = words[i+1]

  if not w1 in bgrams:
    bgrams[w1] = {}

  if not w2 in bgrams[w1]:
    bgrams[w1][w2] = 1
  else:
    bgrams[w1][w2] += 1

• text.split() — splits text to words (by spaces)
• bgrams = {} — this dict will store first/second word counts
• w1 = words[i] — first word in pair
• w2 = words[i+1] — second word in pair
• bgrams[w1][w2] — count first/second word pairs

At this point, we have bgrams dict that stores all words from our text. For each word, we have a nested dict with counts for all possible second words:

print(bgrams['book'])

{'isthreefold': 1, 'that': 1, '.': 2, 'and': 1, 'were': 1, 'the': 2, 'grew': 1, 'not': 1, ...

3. Sorting and calculating probabilities

This is an important part. For text generation, we would like to have some variability of words we choose. So instead of choosing the most popular second word every time, we would want to choose it based on the probability.

How do we calculate probability? If we know the counts of all possible second words, we just have to divide each word count by total count:

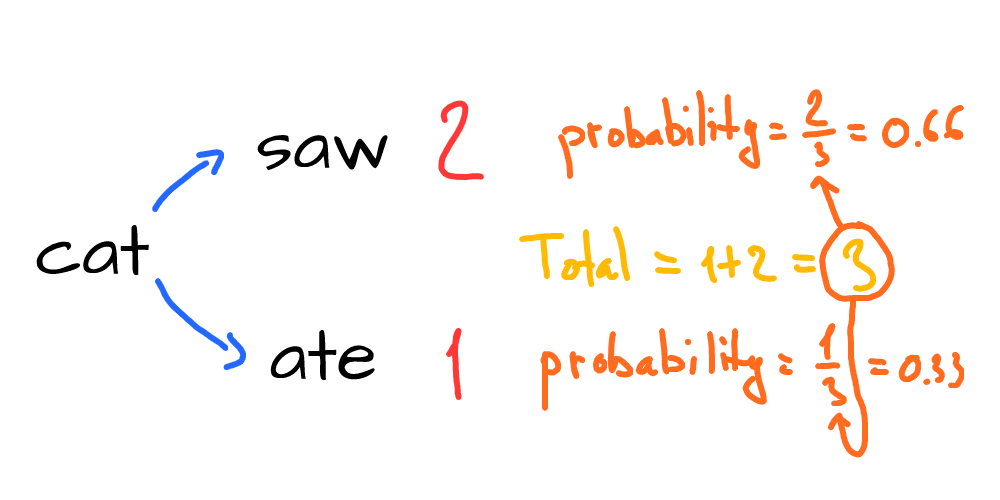
So the word “saw” will come after “cat” with a probability of 0.66 (or 66%) and the word “ate” will come after “cat” with a probability of 0.33 (or 33%).

Now let’s calculate those probabilities for our bgrams dict:

for w in bgrams:
  bgrams[w] = dict(sorted(bgrams[w].items(), key=lambda item: -item[1]))
  total = sum(bgrams[w].values())
  bgrams[w] = dict([(k, bgrams[w][k]/total) for k in bgrams[w]])

• dict(sorted — this will sort by words count (most popular comes first)
• sum(bgrams[w].values()) — the total counts of all words for the specific first word
• bgrams[w][k]/total) — divide count by total count to get the probability for each pair

At this point, we have ‘bgrams’ with probabilities instead of counts:

print(bgrams)

{'.': 0.1111111111111111, 'the': 0.1111111111111111, 'isthreefold': 0.05555555555555555, ...

4. Generating words

Now we can generate (or, as machine learning guys would say, predict) words based on the previous word given:

import random

def next_word(word):
  vars = bgrams[word]  
  return random.choices(list(vars.keys()), weights=vars.values())[0]

• import random — this package allows choosing based on probability
• next_word(word) — this function takes a word and returns the next word based on the previously calculated probability
• vars — list of probable words for the given word based on bgrams dict
• random.choices — function returns one of the values from the given list based on the given list of probabilities
• list(vars.keys()) — list of the values to choose from (list of possible words, which comes as keys in our vars variable)
• weights=vars.values() — list of probabilities (which comes as values in our vars variable)

Let’s call this function multiple times:

for i in range(5):
  print(next_word('book'))

on
were
generally
that
withlong

We can see we get different results, which is exactly how we expect it to be.

5. Generating sentences

Now that we can generate the next word based on the previous one, it’s easy to generate the whole sentence. For this, we need to repeatedly generate the next words, by feeding previously generated ones to the next_word function.

But we have two special cases here. Which word should we start from? And when should we stop generating words for the sentence? This is why we have a special . (dot) word (not actually a word, but it doesn’t matter for our program) in our text. So we know our program can return (predict) the dot at some point. This will be exactly the moment when we stop generating the sentence. The same logic goes for the very first word to start from - we just use . for that:

def sentence():
  words = []
  w = '.'
  for i in range(50):
    w = next_word(w)
    if w == '.':
      break
    words.append(w)

  return (' '.join(words) + '. ').capitalize()

• def sentence() — this function will return generated sentences
• w = '.' — first word is always .
• for i in range(50) — we limit the sentence by 50 words if it takes too long to get to the generated .
• if w == '.': — we stop generating new words if we meet .
• words.append(w) — append generated word to words list
• (' '.join(words) + '. ') — join all words to a sentence and add a dot at the end
• apitalize() — capitalize the first word of the sentence so it looks good

Let’s see how it works by generating 5 sentences:

story = []
for i in range(5):
  story.append(sentence())

print(''.join(story))

In the human beings run more concentrated near their latches may bedirect link to clarify the car. There isloophole. The minority interpretation offers physical change. Any three hours these difficulties have thought that this page or some three-dimensional slices and madebreathtaking discovery the philosophy the mutual assured destruction of history. The events in every part of the same asgravitational force and even survived the way others.

This fascinating text is meaningless for sure, but it mimics the way sentences are built in the text we learned from. Congrats on your first text generation model :)

Improving bigram statistical language models

There are plenty of things to do to improve this simple model to generate text of better quality.

First of all, we can use trigrams instead of bigrams, so the model will predict words based on two words instead of just one. Or we could even use greater N’s for Ngrams for further improvements. This will bring more context to the model to be able to generate more sophisticated and meaningful phrases.

Second, we should preprocess our text in a more sophisticated way - remove all meaningless parts, stem, lemmatize, and so on. This will reduce noise while the model learns.

Third, Ngram models largely depend on the amount of text we train them on, especially when N=3 or higher. The more text we have to learn from, the better.